Кореляція – це статистичний зв’язок між двома біваріантними чи випадковими змінними.
Біваріантні дані (bivariate data), також двовимірні дані – це дані з двох змінних, де кожне значення однієї змінної пов’язане зі значенням іншої змінної.
Визначення міри асоціативності таких змінних залежить від природи даних. Так, наприклад, для категорійних даних використовують таблиці спряженості. Натомість для аналізу кількісних даних використовують коефіцієнт кореляції який ми розглянемо далі більш детально, графічні методи, наприклад, графік розсіювання (scatter plot) чи регресійний аналіз.
Слід зауважити, що коефіцієнт кореляції також може бути застосований до кількісних даних, але за умови, що ці дані піддаються впорядкуванню.
Кількісні дані (quantitative data) – це числові дані які виражають кількісні властивості об’єктів.
Категорійні дані (іноді зустрічається як якісні дані, qualitative data) – це нечислові дані які використовують словесні описи, категорії або мітки для представлення властивостей об’єктів.
Розрізняють кореляцію трбох видів: позитивна, негативна та відсутня. За типом: лінійна, нелінійна.
Позитивна кореляція
Позитивна кореляція вказує на тенденцію двох змінних рости разом. Якщо значення однієї змінної збільшується, то й значення іншої змінної також схильні збільшуватися.
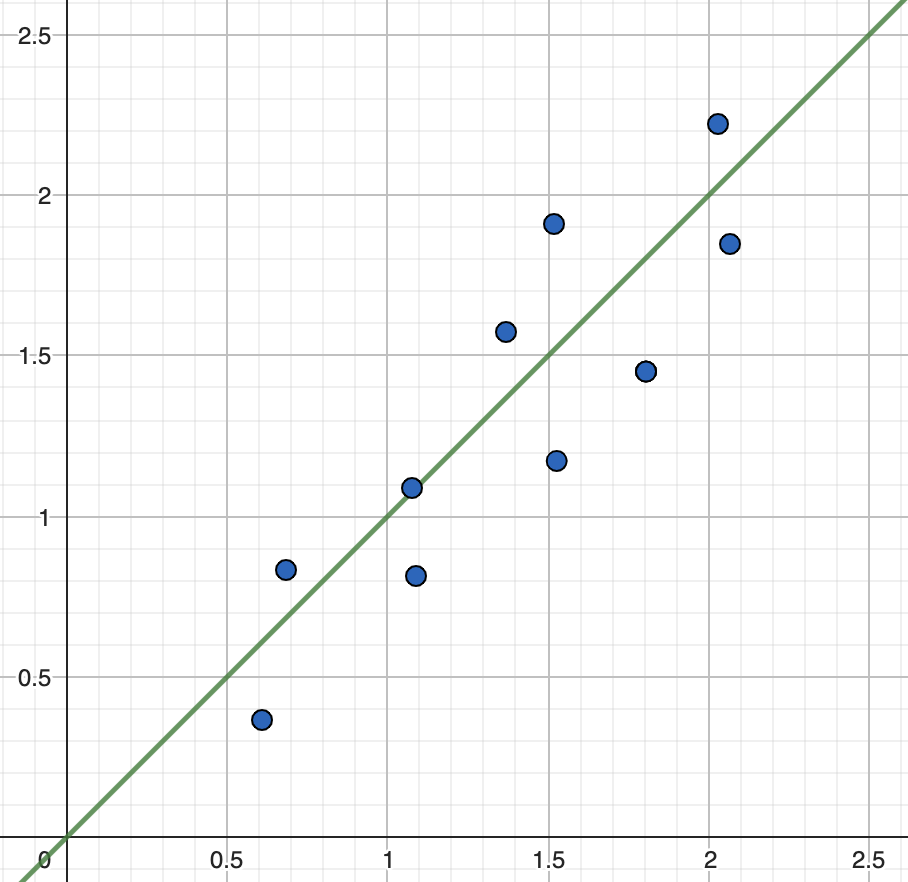
Рис.1. Позитивна лінійна кореляція
Графічно це може бути виражено підняттям лінії тренду.
Негативна кореляція
Негативна кореляція вказує на тенденцію коли значення однієї змінної збільшуються, а значення іншої змінної схильні зменшуватися. Графічно це може бути виражено спуском лінії тренду.
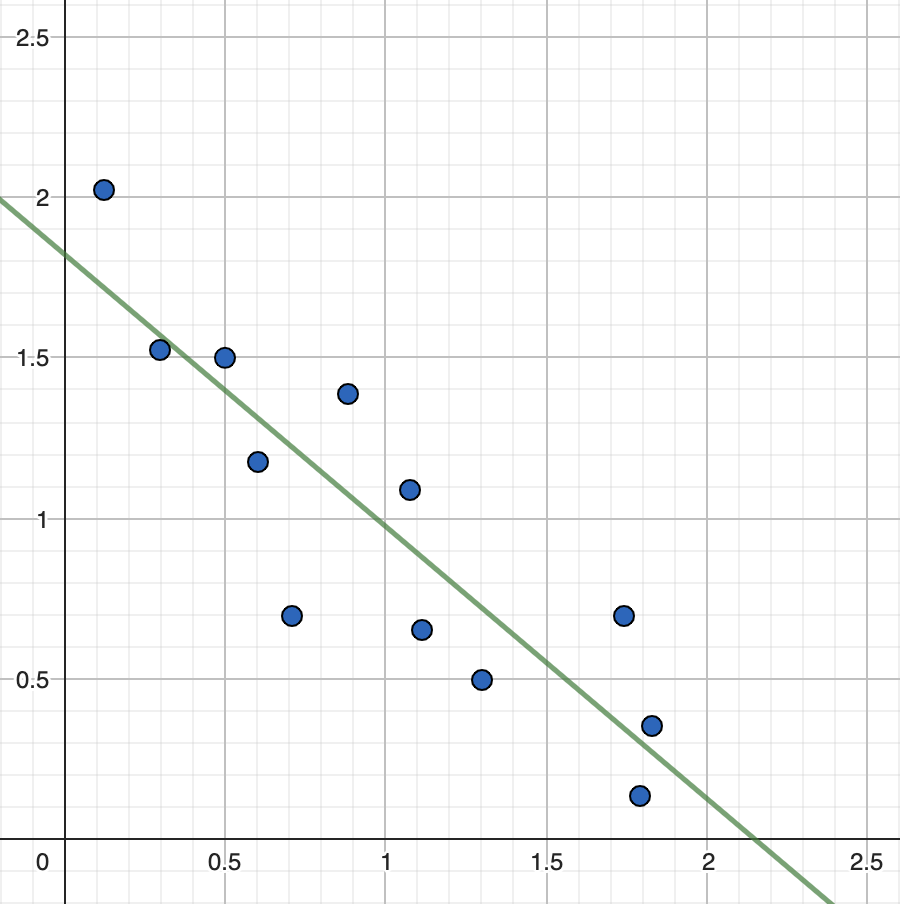
Рис.2. Негативна лінійна кореляція
Відсутня кореляція
Відсутність кореляції за лінійною моделлю (як приклад) вказує на те, що між змінними немає лінійного зв’язку. Це не обов’язково означає, що між змінними взагалі немає взаємозв’язку. Інші типи взаємозв’язків (наприклад, не лінійні) можуть залишатися непоміченими при обчисленні степеня кореляції за допомогою методів, що працюють з лінійними даними.
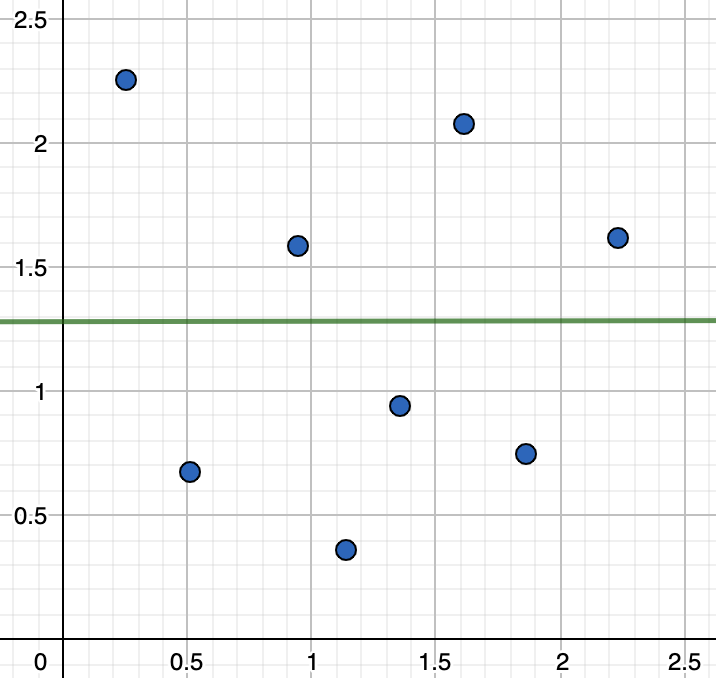
Рис.3. Відсутня лінійна кореляція
Нелінійна кореляція
Нелінійна кореляція вказує на те, що взаємозв’язок між двома змінними не може бути ефективно виражений або апроксимований лінійною моделлю чи прямою лінією. Графічно це може бути виражено довільною кривою.
Коефіцієнт кореляції Пірсона
Для квантування міри (ступеня) кореляції використовують коефіцієнт кореляції. Коефіцієнт кореляції Пірсона rp (іноді просто “кореляція”) – це статистичний показник, який вимірює силу та напрямок лінійної залежності між двома змінними. Припускається, що залежність між змінними можна виразити лінійною функцією.
Значення близьке до 1 вказує на те, що існує пряма асоціація між змінними, близьке до -1 – на зворотну асоціацію, а 0 – на відсутність лінійної залежності.
\[r_p\ =\frac{\sum_{\ i=1}^{\ n}\left(x_i-\overline{x}\right)\cdot\left(y_i-\overline{y}\right)\ }{\sqrt{\sum_{i=1\ }^{n\ }\left(x_i-\overline{x}\right)^2\cdot\sum_{\ i=1}^{\ n}\left(y_i-\overline{y}\right)^2}}\ ,\ де:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\right)\]
\[x_i,\ y_i\ -\ значення\ біваріантних\ змінних\ x\ \ та\ y\ \ для\ спостереження\ i;\]
\[\overline{x},\ \overline{y}\ -\ середнє\ значення\ змінних\ для\ множин\ x\ \ та\ y\ відповіно;\]
Розглянемо обчислення коефіцієнта кореляції Пірсона на прикладі.
Нехай дано чотири біваріантні пари: (25, 30), (30,35), (36, 52), та (45, 71). Розрахуємо основні значення та запишемо результати у таблицю 1.
| xi | yi | xi-x̄ | yi-ȳ | (xi-x̄)2 | (yi-ȳ)2 | (xi-x̄)(yi-ȳ) | |
| 25 | 30 | -9 | -17 | 81 | 289 | 153 | |
| 30 | 35 | -4 | -12 | 16 | 144 | 48 | |
| 36 | 52 | 2 | 5 | 4 | 25 | 10 | |
| 45 | 71 | 11 | 24 | 121 | 576 | 264 | |
| mean | 34 | 47 | |||||
| sum | 222 | 1034 | 475 |
\[r_p\ =\frac{\sum_{\ i=1}^{\ n}\left(x_i-\overline{x}\right)\cdot\left(y_i-\overline{y}\right)\ }{\sqrt{\sum_{i=1\ }^{n\ }\left(x_i-\overline{x}\right)^2\cdot\sum_{\ i=1}^{\ n}\left(y_i-\overline{y}\right)^2}}\ =\frac{475}{\sqrt{222\cdot1034}\ }=\frac{475}{479.11}=\sim0.99\]
Отримане значення вказує на те, що існує стійка позитивна кореляція між змінними x та y: коли x зростає – зростає й y.
Коефіцієнт кореляції Спірмена
Коефіцієнт кореляції Спірмена rs, запропонований англійським психологом Чарльзом Спірменом, дозволяє визначити силу та напрямок монотонної залежності між двома змінними: оцінює ступінь монотонного взаємозв’язку, тобто, чи одна змінна загалом зростає або зменшується, коли інша змінюється.
\[r_s\ =1-\frac{6\cdot\sum_{i=1}^nd_i^2}{n\left(n^2-1\right)}\ ,\ де:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\right)\]
\[n\ -\ кількість\ біваріантних\ пар;\]
\[d^2\ -\ квадрат\ різниці\ рангів\ біваріантних\ пар;\]
Коефіцієнт кореляції Спірмена – це число у діапазоні −1 ≤ rs ≤ 1. Значення, близькі до -1 чи 1, вказують на сильну монотонну залежність, а 0 – на відсутність монотонної залежності. Розглянемо обчислення коефіцієнту rs для кількісних даних на прикладі.
Нехай дано три біваріантні пари: (2, -3), (5,4), (-6, 1).
Обчислимо ранги для множин змінних і запишемо результат у таблиці 2.
Ранг – порядковий номер позиції значення змінної у впорядкованому масиві. Для набору спостережень ранги присвоюються кожному значенню відповідно до його порядку у відповідному впорядкованому масиві.
Наприклад, наша множина змінних xi = {2, 5, -6} після сортування виглядає таким чином: xi = {-6, 2, 5}. Ранги будуть відповідати позиціям у цьому відсортованому ряді: для -6 ранг буде 1, для 2 – 2, для 5 – 3. Для множини yi = {-3, 4, 1} впорядкований масив виглядає так: yi = {-3, 1, 4}, де: для -3 ранг буде 1, для 1 – 2, для 4 – 3. Отже:
| x | Rx | y | Ry | d | d2 |
| 2 | 2 | -3 | 1 | 1 | 1 |
| 5 | 3 | 4 | 3 | 0 | 0 |
| -6 | 1 | 1 | 2 | -1 | 1 |
\[r_s=1-\frac{6\cdot\sum_{i=1}^nd_i^2}{n\left(n^2-1\right)}=1-\frac{6\cdot\left(1+0+1\right)}{3\left(3^2-1\right)}=1-\ \frac{12}{27-1}=1-\frac{12}{26}=\sim0.54\]
Кореляція Пірсона vs. Спірмена
Підсумуємо основні властивості обох методів у таблиці 3.
| Властивість | коефіцієнт Пірсона | коефіцієнт Спірмена |
| Діпазон | [1,-1] | [1,-1] |
| Тип ассоціативності даних | лінійний | монотонний |
| Тип розподілу даних | нормальний розподіл | також ненормальний або порядковий |
| Чутливість до аномальних даних | чутливий | менш чутливий |
| Метод обчислення | стандартне відхилення, коваріативність | ранжування |
Кореляція – не причина
Часто кореляцію плутають із причиною. Це доволі поширена логічна хиба про причинно-наслідковий зв’язок. Розглянемо можливі типи причинно-наслідкового зв’язку та кореляції.
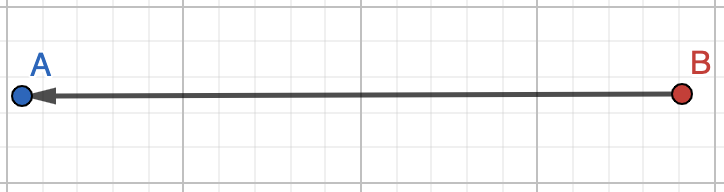
Між змінними A та B існує кореляція, одна із змінних зпричиняє іншу. Між ними існує причинно-наслідковий зв’язок.
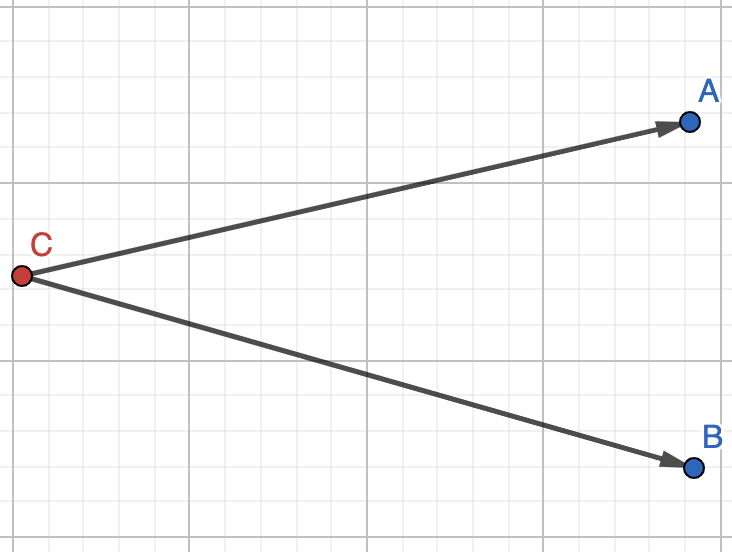
Між змінними A та B існує кореляція, проте обоє зпричинені іншою змінною (фактором). Між A і B не існує прямого причинно-наслідкового зв’язку, але існує між С та A і С та B.
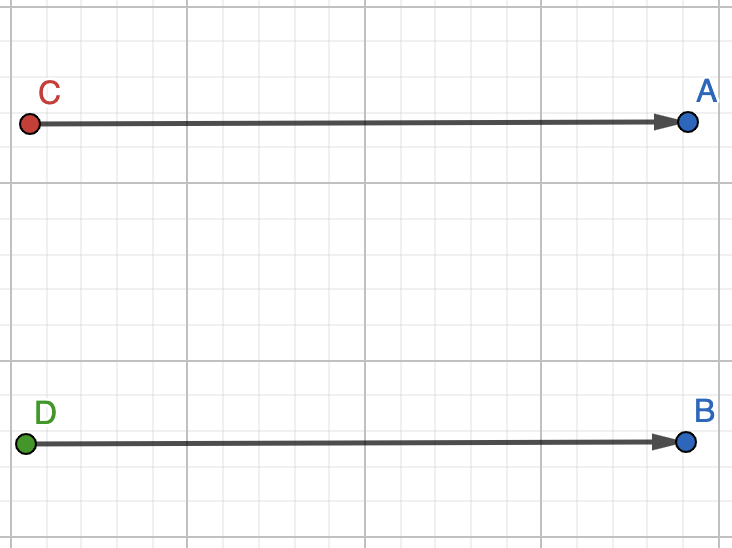
Між змінними A та B існує кореляція, A зпричинене С, а B – D. A та B непов’язані змінні, наявність кореляції – збіг.
Cum hoc ergo propter hoc (лат. «разом із цим, отже, внаслідок цього») – логічна хиба сумнівної причинності, в якій збіг обставин або кореляція між певними ознаками приймається за доказ причиново-наслідкового зв’язку без додаткової перевірки причинності.
wikipedia.org
Слід зауважити, що в статті ми розглянули методи обчислення коефіцієнта кореляції для лінійних біваріантних даних. Для нелінійних даних можуть використовувати інші методи такі як: коефіцієнт кореляції Кендала, кореляція відстаней тощо.