Теорема Баєса була вперше запропонована англійським математиком Томасом Баєсом (Thomas Bayes) в 1793 році у праці “An essay towards solving a problem in the doctrine of chances.” та далі розвинута П. Лапласом в його праці “Théorie analytique des probabilités” у 1812 році. Теорема Баєса описує ймовірність події, спираючись на обставини (свідчення), що могли би бути пов’язані з цією подією.
Твердження Апріорі та Апостеріорі
Наші знання про щось можна поділити на два умовні типи за походженням: знання які ми отримали через досвід (особистий, колективний, експеримент тощо) та суб’єктивні знання які грунтуються на нашому припущенні чи інтуїції. Спробуємо формалізувати ці два типи знань не вдаючись у філософський дискурс питання.
Апріорі (лат. a priori — первісно) — те, що передує досвіду.
uk.wikipedia.org
Апостеріо́рі (лат. a posteriori) — те, що випливає з досвіду.
uk.wikipedia.org
Узгодимо основні скорочення:
\[H\ -\ hypothesis\ -\ гіпотеза;\ E-evidence\ -\ свідчення,\ чи\ дані\ у\ ширшому\ контексті;\]
В машинному навчанні ми часто намагаємося вибрати найкращу гіпотезу апріорі H на основі свідчень E. Теорема Баєса дозволяє розразхувати ймовірність гіпотези на основі відомостей які можуть бути повязані із нею.
\[P(H|E)=\frac{P(E|H)\cdot P(H)}{P(E)},\ \ де:\]
\[P(H)-апріорна\ ймовірність\ настання\ події\ H\ \left(незалежно\ від\ відомостей\ E\right);\]
\[P(E)-ймовірність\ настання\ події\ E\ \left(незалежно\ від\ гіпотези\ H\right);\]
\[P(H∣E)-це\ апостеріорна\ імовірність\ правдивості\ гіпотези\ H\ після\ отримання\ нових\ відомостей\ E;\]
\[P(E∣H)-ймовірність\ того,\ що\ E\ станеться,\ якщо\ гіпотеза\ H\ правдива;\]
P(H|E) та P(E|H) є умовними ймовірностями.
Умо́вна ймові́рність — ймовірність однієї події за умови, що інша подія вже відбулася.
uk.wikipedia.org

Оскільки теоретичний опис виглядає дещо складним, спробуємо поглянути на метод Баєса з практичної точки зору.
Приклад 1. Наївний Баєс як спам-фільтр.
Розглянемо теорему Баєса на прикладі спам-фільтру електронних повідомлень. Оскільки, ми працюємо із поняттями спам/не спам повідомлення та слово в повідомленні, для зручності уточнимо поняття гіпотези та свідчення і виконаємо їх схематичну заміну. Отже:
\[Гіпотеза\ H\ -повідомлення\ є\ спамом\ S:\ P\left(H\right)\ замінимо\ на\ P\left(S\right)\ \]
\[Гіпотеза\ \neg H\ -повідомлення\ не\ є\ спамом\ S:\ P\left(\neg H\right)\ замінимо\ на\ P\left(\neg S\right)\ \]
Нехай дано масив повідомлень довжиною L = 10. Якщо ми не володіємо жодною інформацією про природу повідомлень в масиві, ми можемо припустити, що половина повідомлень є спам-повідомленнями, а інша половина – нормальними повідомленнями. Проте, для покращення роботи нашого фільтра, ми провели експертну оцінку вмісту повідомлень у навчальній вибірці, і тепер можемо зробити апріорне припущення про його вміст. Так, масив містить 4 спам-повідомлення та 6 нормальних повідомлень. Отже, можна стверджувати, що випадково вибране повідомлення з тестової вибірки може бути спам-повідомленням з йомвірністю 0.4 або 40%:
\[P\left(S\right)\ =\ \frac{4}{10}=\frac{2}{5}=0.4;\ P\left(\neg S\right)\ =\ \frac{6}{10}=\ \frac{3}{5}=0.6;\ \]
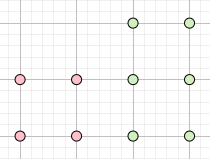
Рис.2. Масив повідомлень складається з 4-х cпам повідомлення та 6-и нормальних повідомлень.
Спробуємо переоцінити ймовірності за умови, що нам відомо одне слово із повідомлення. Іншими словами: яка ймовірність того, що вибране повідомлення є спам-повідомленням, якщо вибране слово w із цього повідомлення притаманне спам-повідомленням. Формально, цe можна записати як апріорну ймовірність (після перевірки гіпотези – слово притаманне спам-повідомленням):
\[P\left(S∣w\right)\]
Для цього нам потрібно розрахувати величини P(w∣S) та P(w∣¬S). Де:
\[P(w∣S)\ -\ ймовірність\ того,\ що\ слово\ w\ належить\ спам\ повідомленню;\]
\[P(w∣\neg S)\ -\ ймовірність\ того,\ що\ слово\ w\ не\ належить\ спам\ повідомленню;\]
Проаналізувавши наші повідомлення ми встановили, що слово w (скажімо, “money”) є присутнє у 2-х спам повідомленнях та 1-му нормальному повідомленні.
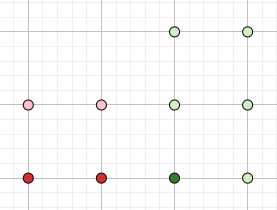
Рис 3. Повідомлення які містять вибране слово w.
Звідси:
\[P(w∣S)\ =\ \frac{2}{4}=0.5;\]
\[P(w∣\neg S)\ =\ \frac{1}{6}=0.1666;\]
Підсумуємо наші обчислення і запишемо їх в таблицю для наочності.
| P(S) | 0.4 |
| P(¬S) | 0.6 |
| P(w∣S) | 0.5 |
| P(w∣¬S) | 0.1666 |
\[P(S|w)=\frac{P(w|S)\cdot P(S)}{P(w)}=\frac{P(w|S)\cdot P(S)}{P(w|S)\cdot P(S)+P(w|\neg S)\cdot P(\neg S)}=\frac{0.5\cdot0.4}{0.5\cdot0.4+0.1666\cdot0.6}=\]
\[=\frac{0.2}{0.2\ +0.0999}=\frac{0.2}{0.2999}=\sim0.67\]
Отже результат можна підсумувати так: якщо у вибраному повідомленні присутнє слово w, то існує ймовіріність рівна 0.67 або 67%, що дане повідомлення є спам-повідомленням. Зауважте, як змінилась ймовірність у порівнянні з початковим припущенням апріорі – 40%. Якщо виконати такі обчислення для кожного слова з повідомлення то ми отримаємо спрощений варіант наївного спам-класифікатора Баєса. Слово наївний означає те, що класифікатор не вразовує жодного зв’язку між словами (семантичного, лексичного тощо).
Приклад 2. Тест на антитіла до COVID-19 .
Розглянемо як метод Баєса може бути використаний для оцінки ймовірності захворювання на вірус SARS-CoV-2 за допомогою тесту на антитіла. Припустимо, існує умовне місто X для якого відомо, що 10% його мешканців хворіють на ковід.
Нехай існує тест на визначення вірусу в якого чутливість – 99.8% , а специфічність – 97%.
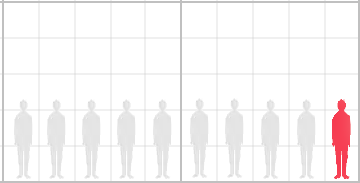
Рис 4. Мешканці умовного міста.
За аналогією із першим прикладом виконаємо заміну змінних для простоти:
\[Гіпотеза\ H\ -людина\ хвора\ на\ ковід\ C:\ P\left(H\right)\ замінимо\ на\ P\left(C\right)\ \]
\[Гіпотеза\ \neg H\ -людина\ не\ хвора\ на\ ковід\ C:\ P\left(\neg H\right)\ замінимо\ на\ P\left(\neg C\right)\]
\[P(sp∣U)\ -\ ймовірність\ того,\ що\ людина\ є\ інфікована\ і\ може\ бути\ виявлена\ тестом;\]
\[P(sp∣\neg U)\ -\ ймовірність\ того,\ що\ людина\ не\ є\ інфікована\ і\ може\ бути\ виявлена\ тестом\ помилково;\]
\[P(sp|С)\ =\ специфічність\ =\ 0.97\]
\[P(sp∣\negС)\ \ =\ \left(1-специфічність\right)=0.03\]
Підсумуємо наші обчислення і запишемо їх в таблицю для наочності.
| P(C) | 0.1 |
| P(¬C) | 0.9 |
| P(sp|С) | 0.97 |
| P(sp∣¬С) | 0.03 |
\[P(C|sp)=\frac{P(w|S)\cdot P(S)}{P(w)}=\frac{P(sp|C)\cdot P(C)}{P(sp|C)\cdot P(C)+P(sp|\neg C)\cdot P(\neg C)}=\frac{0.97\cdot0.1}{0.97\cdot0.1+0.03\cdot0.9}=\]
\[=\ \frac{0.097}{0.097+0.027}=\frac{0.097}{0.124}=0.7822\]
Незважаючи на те, що тест здається дуже точним, кількість здорових людей у вибірці значно переважає кількість хворих. Отже навіть якщо індивід отримав позитивний результат тесту, ймовірність складає ~78%. Чому? Кількість здорових людей суттєво переважає кількість людей хворих на ковід (припущення апріорі). Тому кількість помилково позитивних результатів переважатиме над кількістю істинно позитивних.
З прикладів випливає ключова властивість методу Баєса – це можливість використовувати попередні знання у вигляді апріорної ймовірісності в чисельнику теореми Баєса кожного разу інкрементально перераховуючи ймовірності по мірі появи нових свідчень (даних). Так, зробивши другий тест з оновленими початковими ймовірностями, ми вже отримуємо ймовірність близьку 90%.
\[P(C|sp)=\frac{P(w|S)\cdot P(S)}{P(w)}=\frac{P(sp|C)\cdot P(C)}{P(sp|C)\cdot P(C)+P(sp|\neg C)\cdot P(\neg C)}=\frac{0.97\cdot0.2178}{0.97\cdot0.2178+0.03\cdot0.7822}=\]
\[=\ \frac{0.2124}{0.2124+0.0234}=\frac{0.2124}{0.2358}=\sim0.90\]
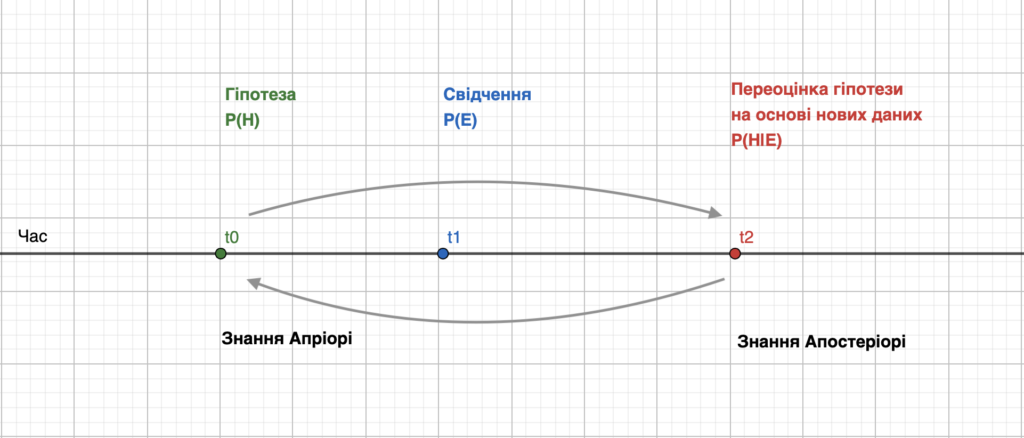
В своїй основі суть методу Баєса відповідає інтуєтивній властивісті розуму: висунути апріорну гіпотезу про щось, а тоді здійснити її переоцінку кожного разу як з’являються нові відомості які пов’язані із нею.