Поняття інформаційної ентропії було введено Клодом Шенноном у його праці “Математична теорія зв’язку“. Ентропія Шенона слугує визначником (мірилом) невизначеності стану джерела повідомлень (системи). В теорії інформації ентропія системи характеризує середній ступінь невизначеності стану цього джерела серед усіх можливих її станів.
Існують й інші види ентропії як от, наприклад, міні-ентропія яка використовується у криптографії, кросс-ентропія тощо.
Спробуємо зрозуміти ентропію через явище здивування.
Явище здивування
Ентропія в інформаційних системах пов’язана із ймовірністю настання події та здивуванням або інформаційним змістом від події (information content). Існує оберенена залежність між ймовірністю настання події та поняттям здивування. Якщо ймовірність настання події є висока то здивування – низьким і навпаки.
Явище здивування вводиться у вжиток через логічний зв’язок невизначеність -> несподіваність -> подія -> здивування.
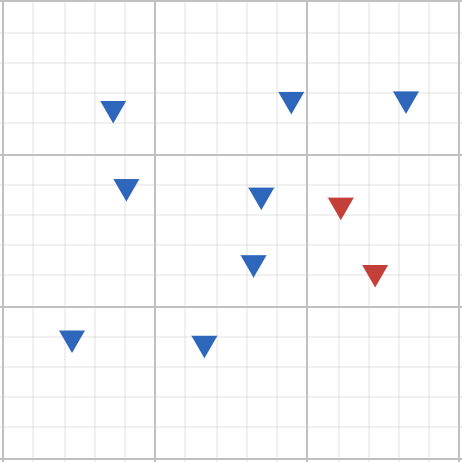
Система А, що складається із восьми синіх та двої червоних трикутників.
Так, наприклад, для системи A, ймовірність витягнути червоний трикутник є низькою, а отже і здивування при її витягуванні – високим.
Явище здивування є інтуєтивно зрозуміле проте дещо штучне. Воно слугує визначником того на скільки інформативним є настання події (значушчим) по відношенню до уявлення про природу події та початкові очікування щодо її настання, та, вцілому, пов’язана із теоремою Баєса.
Спробуємо представити залежність між здивуванням та ймовірністю настання події більш формалізовано.
\[S\left(x\right)\ =\ \frac{1}{p\left(x\right)},\ де:\]
\[S\left(x\right)\ -\ здивування\ від\ події\ x,\ p\left(x\right)\ -\ ймовірність\ настання\ події\ x;\]
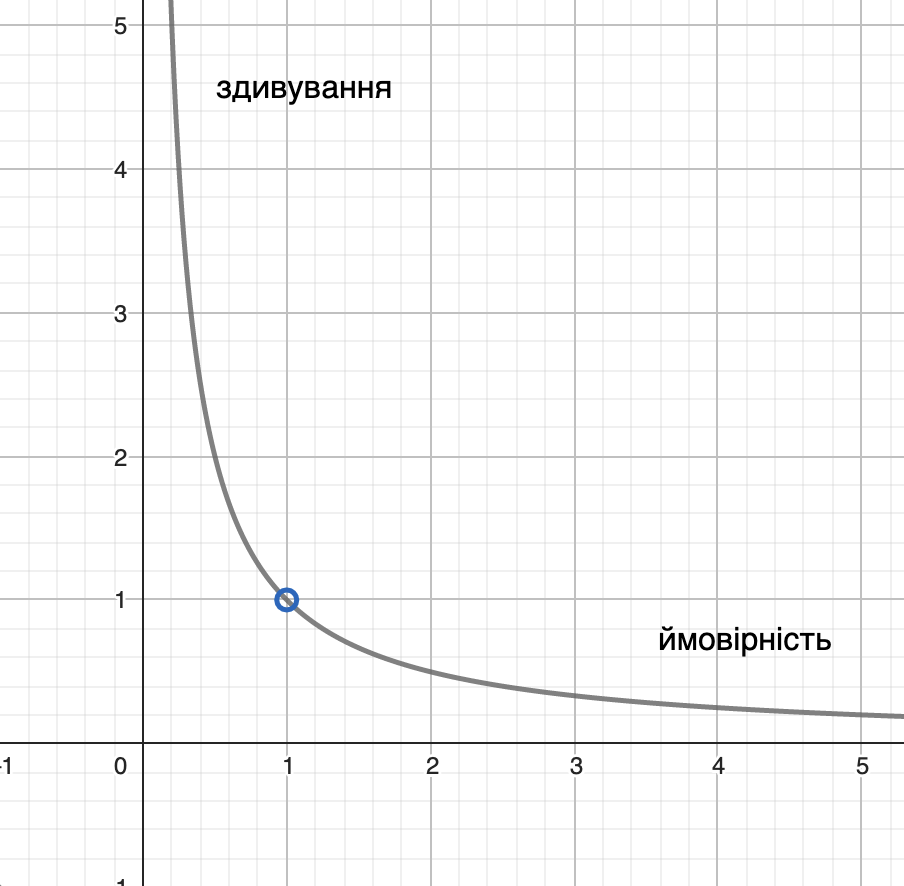
Графічне представлення оберненої залежності здивування та ймовірності
Проте в такої залежності є один суттєвий недолік. Для тих випадків коли ймовірність настання події рівна 1, наша залежність поверне значення очікування також рівне 1. Власне кажучи, це не те значення здивування яке ми очікуємо при настанні такого типу події. Навпаки, здивування в цьому випадку повинне бути рівне 0. Щоб усунути цей недолік, використаємо логарифмічну функцію, оскільки:
\[\log\left(1\right)\ =\ 0;\ \log\left(0\right)\ =\ undefined;\]
\[S\left(x\right)\ =\ \log_a\left(\frac{1}{p\left(x\right)}\right),\ де\ a-\ кількість\ станів\ системи\]
Таким чином, для бінарної ймовірнісної системи, здивування можна записати як:
\[S\left(x\right)\ =\ \log_2\left(\frac{1}{p\left(x\right)}\right)\]
В статистиці ентропію визначають як суму очікуваних значень здивування для всіх можливих подій у системі.
\[E\left(X\right)\ =\ \sum_{\ }^{\ }S_x\cdot p\left(x\right)=\sum_{\ }^{\ }\log\left(\frac{1}{p\left(x\right)}\right)\cdot p\left(x\right),\ \ де:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\right)\]
\[-\ S_x-здивування\ від\ настання\ події\ x;\ p\left(x\right)\ -\ ймовірність\ настання\ події\ x\]
Така формула дещо відрізняється від загальноприйнятої, а тому може бути спрощена як:
\[E=\sum_{\ }^{\ }\log\left(\frac{1}{p\left(x\right)}\right)\cdot p\left(x\right)\ =\ \sum_{\ }^{\ }p\left(x\right)\ \cdot\log\left(\frac{1}{p\left(x\right)}\right)\ =\]
\[=\sum_{\ }^{\ }p\left(x\right)\ \cdot\left(\log\left(1\right)-\log\left(p\left(x\right)\right)\right)\ =\ \sum_{\ }^{\ }p\left(x\right)\ \cdot\left(0-\log\left(p\left(x\right)\right)\right)\ =\]
\[=-\sum_{\ }^{\ }p\left(x\right)\ \cdot\log\left(p\left(x\right)\right)\ =-\sum_{\ i}^{\ C}p_i\ \cdot\log\left(p_i\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\right)\]
Спробуємо порахувати ентропію трьох різних систем A, B та С за допомогою формули (1).
Система A.

Система А. 8С + 2Ч.
Оскільки в системі А загальна кількість об’єктів – десять, вісім з яких сині, а два – червоні то ймовірності витягування трикутників відповідних кольорів становлять 0.8 та 0.2 відповідно. Порахуємо величину здивування, а результ запишимо в таблицю 1. Повторимо відповідні дії для систем B та С.
\[p_A\left(x_c\right)\ =\ \frac{8}{10}=0.8;\ \ p_A\left(x_ч\right)\ =\ \frac{2}{10}=0.2;\]
\[S_A\left(x_c\right)\ =\log_2\left(\frac{1}{0.8}\right)\ \ =\ 0.3219;\ S_A\left(x_ч\right)\ =\log_2\left(\frac{1}{0.2}\right)\ \ =\ 2.3219;\ \]
\[E\left(A\right)\ =\ 0.8\cdot0.3219\ +\ 0.2\cdot2.3219\ =\ 0.2575+\ 0.4644\ =\ 0.7219\]
| Колір | Ймовірність | Здивування |
| Синій | 0.8 | 0.3219 |
| Червоний | 0.2 | 2.3219 |
Ентропія системи A – 0.7219
Система B.
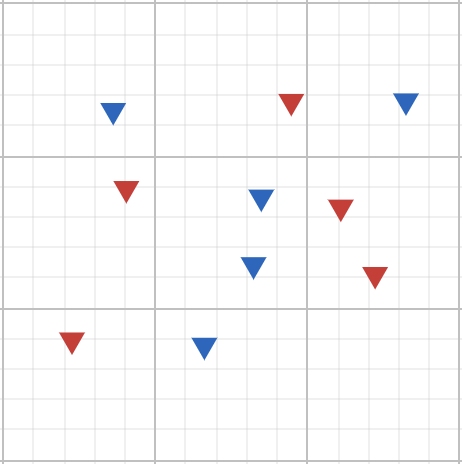
Система B. 5С + 5Ч.
\[p_B\left(x_c\right)\ =\ \frac{5}{10}=0.5;\ \ p_B\left(x_ч\right)\ =\ \frac{5}{10}=0.5;\]
\[S_B\left(x_c\right)\ =\log_2\left(\frac{1}{0.5}\right)\ \ =\ 1;\ S_B\left(x_ч\right)\ =\log_2\left(\frac{1}{0.5}\right)\ \ =\ 1;\ \]
\[E\left(B\right)\ =\ 0.5\cdot1\ +\ 0.5\cdot1\ =\ 1\]
| Колір | Ймовірність | Здивування |
| Синій | 0.5 | 1 |
| Червоний | 0.5 | 1 |
Ентропія системи B – 1
Система С.
Cистема С. 0С + 10Ч.
\[p_C\left(x_c\right)\ =\ \frac{0}{10}=0;\ \ p_C\left(x_ч\right)\ =\ \frac{10}{10}=1;\]
\[S_C\left(x_c\right)\ =\log_2\left(\frac{1}{0}\right)\ \ =\ undefined;\ S_C\left(x_ч\right)\ =\log_2\left(\frac{1}{1}\right)\ \ =\ 0;\ \]
\[E\left(C\right)\ =\ undefined\cdot0\ +\ 1\cdot0\ =\ undefined\]
| Колір | Ймовірність | Здивування |
| Синій | 0 | undefined |
| Червоний | 1 | 0 |
Ентропія системи C – 0 (невизначена)
Ентропія в теорії інформації вимірює рівень невизначеності чи несподіваності в системі. Якщо система завжди перебуває у тому ж самому стані або генерує ту саму інформацію, то немає ніякої невизначеності, і її ентропія дорівнює нулю.
Приклад визначення ентропії стохастичного джерела даних
Обчислимо ентропію функції-генератора випадкових чисел numpy.random.randint за допомогою формули (2) яка генерує три випадкові величини: 0,1,2 (має три стани). Обчислення здійснюємо після того як отримаємо інформацію довжиною 1000 елементів.
In [1]: import math
In [2]: import numpy as np
In [3]: states = 3
In [4]: predictions = 1000
In [5]: data = np.array([np.random.randint(states) for _ in range(predictions)])
In [6]: data[:10]
Out[6]: array([0, 0, 2, 2, 2, 1, 0, 0, 0, 1])
In [7]: pA = np.sum(data == 0) / len(data)
In [8]: pB = np.sum(data == 1) / len(data)
In [9]: pC = np.sum(data == 2) / len(data)
In [10]: pA, pB, pC
Out[10]: (0.35, 0.32, 0.33)
In [11]: entropy = lambda probability: probability*math.log(probability, states)
In [12]: print(f"Random function entropy is {-1 * sum(map(entropy, [pA, pB, pC]))}")
Random function entropy is 0.9993656466540995Eнтропія функції є високою і становийть 0.9993 (~1), Це говорить нам про те, що вона характеризується висовим рівнем невизначеності, що відповідає її призначенню.