Приріст інформації, також відомий як розходження інформації – важлива метрика оцінки якості розподілу об’єктів в задачах класифікації та регресії.
Обчислення приросту інформації використовується для оцінки якості розбиття даних (split quality) в таких відомих класифікаторах як-от, наприклад, RandomForest (Випадковий Ліс), DecisionTree (Дерево Рішень) поряд із іншими відомими методами, наприклад, Gini Impurity та LogLoss.
Читати більше про Gini Impurity та LogLoss.
Приріст інформації – це різниця між ентропією початкового набору даних та зваженою ентропією підмножин даних після поділу за атрибутом даних. Існує велика кількість способів математичного запису приросту інформації, але зупинемось на цьому:
\[G\left(A,S\right)=E\left(S\right)\ -\ H\left(A,S\right)\ =E\left(S\right)-\sum_{j=1}^v\frac{S_j}{S}\cdot E\left(S_j\right),\ де\ \ \ \ \ \ \ \ \ \left(1\right)\ \]
\[\ E\left(S\right)\ -\ ентропія\ початкового\ набору\ даних;\]
\[H\left(A,\ S\right)\ -\ зважена\ ентропія\ підмножин\ даних\ після\ поділу\ за\ атрибутом\ A;\]
\[v\ -множина\ унікальних\ значень\ атрибуту\ A;\]
\[E\left(S_j\right)-\ ентропія\ підмножини\ даних\ після\ поділу\ за\ атрибутом\ A;\]
\[S\ -\ загальна\ кількість\ екземплярів\ в\ наборі\ даних;\]
\[S_j-кількість\ екземплярів\ зі\ значенням\ j\ атрибуту\ A;\]
На перший погляд, формула виглядає доволі складно, але її зміст та значення насправді є інтуїтивно зрозумілі. Спробуємо розглянути суть приросту інформації на прикладах.
Ентропія
Обчислення приросту інформації базуються на ідеї інформаційної ентропії. У статті “Eнтропія в інформаційних системах” ви можете більше детально ознайомитись із формулою та її поясненням через концепцію “здивування”. Тут лише коротко наведемо формулу ентропії запропоновану К. Шеноном.
\[E\ =\ -\sum_{\ i}^{\ C}p_i\cdot\log_b\left(p_i\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\right)\]
Зв’язок між ентропією та інформаційний приростом
Уявімо систему X яка складається з шести елементів двох можливих кольорів (b=2).
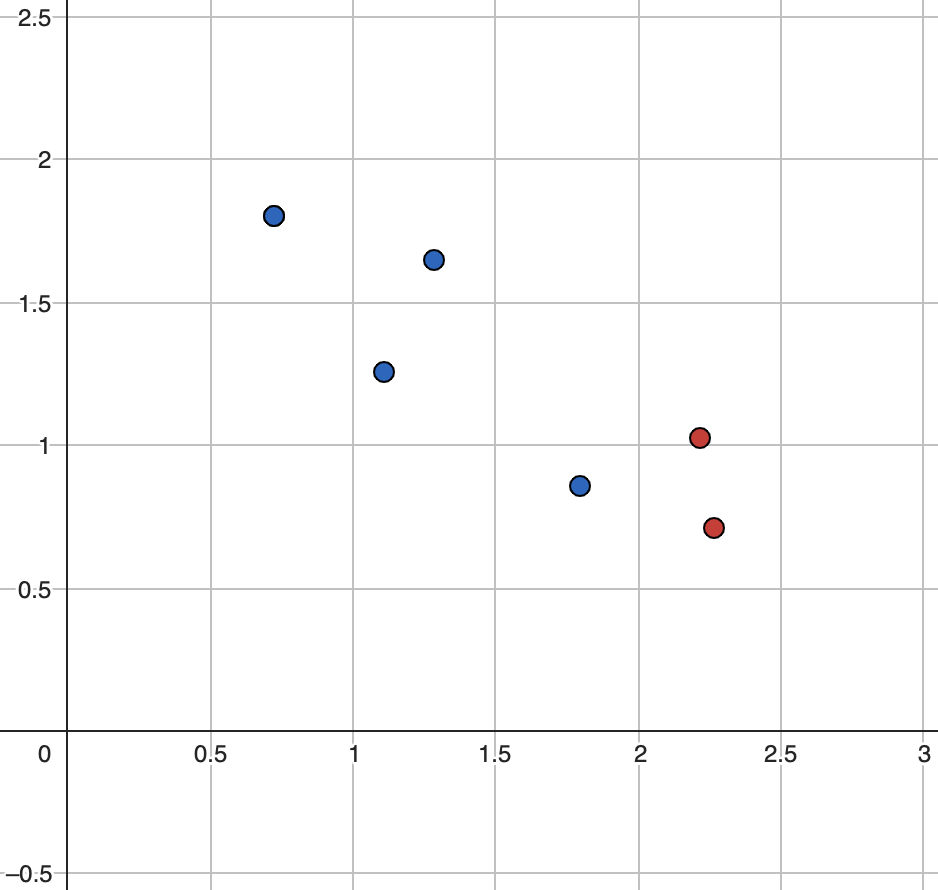
Порахуємо ентропію системи X.
\[p\left(с\right)\ =\ \frac{4}{6}=\frac{2}{3};\ p\left(ч\right)\ =\ \frac{2}{6}=\frac{1}{3};\ b=2;\]
\[E_{parent}\ =\ -\sum_{\ i}^{\ C}p_i\cdot\log_b\left(p_i\right)=-1\cdot\left(\frac{2}{3}\cdot\log_2\left(\frac{2}{3}\right)\ +\frac{1}{3}\cdot\log_2\left(\frac{1}{3}\right)\right)\ =\]
\[=-1\cdot\left(-0.39+\left(-0.53\right)\right)=\sim0.92\]
Отже, початкова ентропія нашої системи складає 0.92. Якби наша система складалась із одноколірних елементів то її ентопія становила б 0. Якби система складалась із одинакової кількості різноколірних елементів то її ентропія була б близька до 1. Оскільки отримане значення – 0.92 це вказує на дві речі. По-перше, система характеризується невизначеною. По-друге, невизначеність не є однорідною, тобто існують неодинакові ймовірності отримати різноколірні елементи.
Тепер уявимо, що існує якась функція Y яка намагається оптимально розділити два набори кульок (класифікувати оптимально).
Графічне представлення функції наведено нижче. З рисунку стає зрозуміло, що функція поділила простір неоптимально, але близько до оптимального. Постає питання, як оцінити якісь розбиття математично?
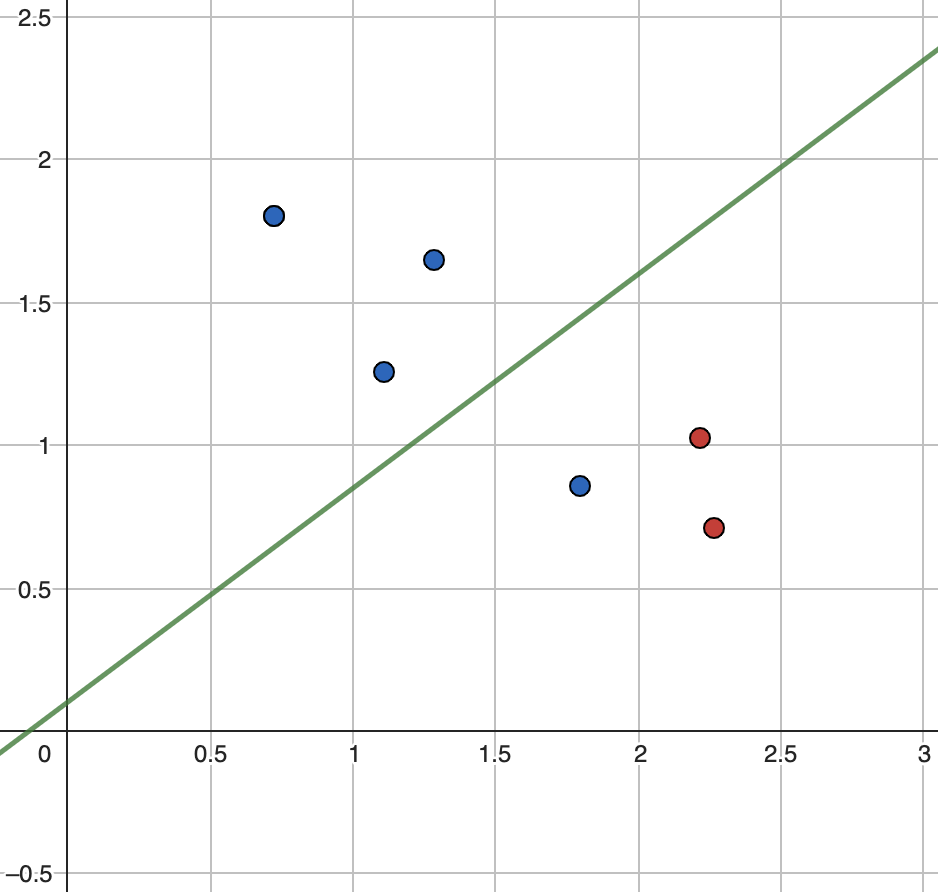
Оскільки ми отримали два різні набори даних, розрахуємо ентропію для кожного із них.
\[E_{top}=-1\cdot\left(\frac{3}{3}\cdot\log_2\left(\frac{3}{3}\right)\right)\ =-1\left(1\cdot\log_2\left(1\right)\right)\ =0\]
\[E_{bottom}=-1\cdot\left(\frac{1}{3}\cdot\log_2\left(\frac{1}{3}\right)\ +\frac{2}{3}\cdot\log_2\left(\frac{2}{3}\right)\right)\ \ =\sim0.92\]
Тепер порахуємо загальну зважену ентропію (із врахуванням к-сть елементів у групі) системи X після розбиття.
\[\ E_{split}=\frac{3}{6}\cdot0\ +\ \frac{3}{6}\cdot0.92=0.46\]
Отже, після розбиття простору на два кластери ентропія системи знизилась до 0.46. Таким чином, приріст інформації складає:
\[G_1\ =\ 0.92\ -\ 0.46\ =\ 0.46\]
Задамо дві нові фyнкції розбиття Y та обчислимо нові значення:
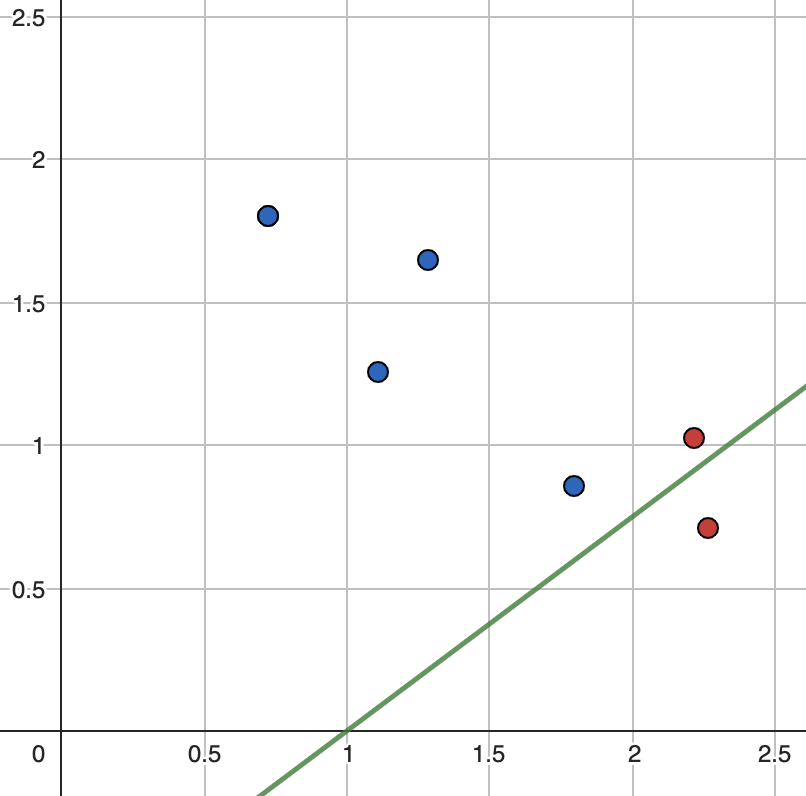
\[E_{top}=-1\cdot\left(\frac{1}{6}\cdot\log_2\left(\frac{1}{6}\right)\right)\ =-1\cdot\left(1\cdot\log_2\left(1\right)\right)\ =0\]
\[E_{bottom}=-1\cdot\left(\frac{4}{5}\cdot\log_2\left(\frac{4}{5}\right)\ +\frac{1}{5}\cdot\log_2\left(\frac{1}{5}\right)\right)\ \ =\sim0.72\]
\[\ E_{split}=\frac{5}{6}\cdot0.72\ +\ \frac{1}{6}\cdot0=\sim0.6\]
\[G_2\ =\ 0.92\ -\ 0.6\ =\ 0.32\]
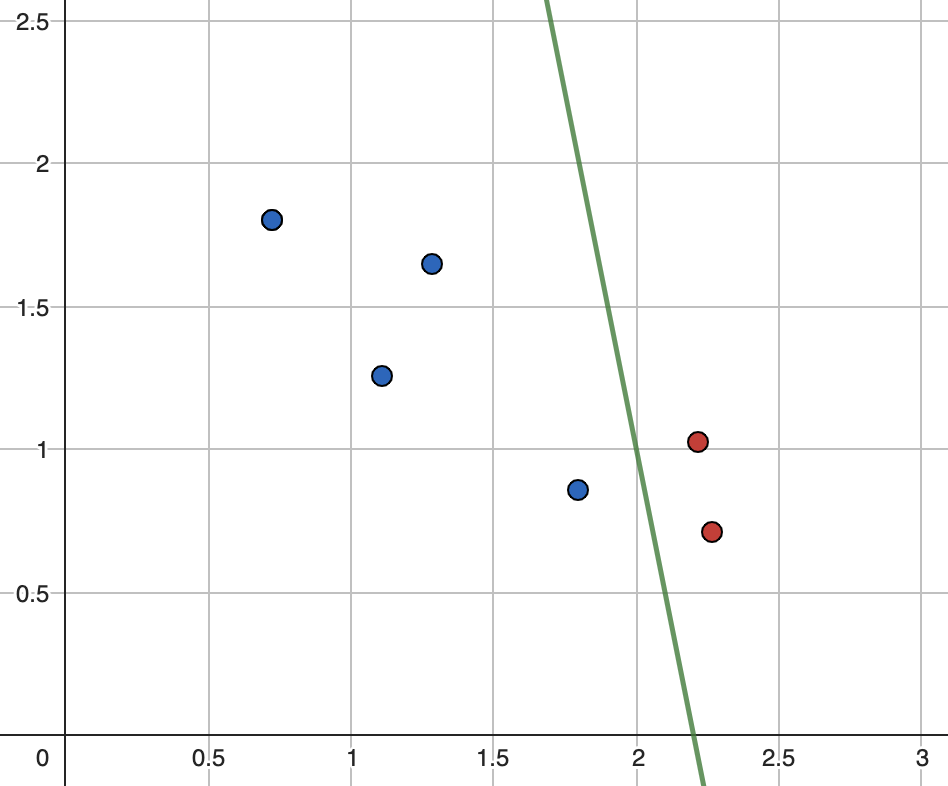
\[E_{left}=-1\cdot\left(\frac{4}{4}\cdot\log_2\left(\frac{4}{4}\right)\right)\ =-1\left(1\cdot\log_2\left(1\right)\right)\ =0\]
\[E_{right}=-1\cdot\left(\frac{2}{2}\cdot\log_2\left(\frac{2}{2}\right)\ \right)\ \ =-1\left(1\cdot\log_2\left(1\right)\right)\ =0\]
\[\ E_{split}=\frac{4}{6}\cdot0\ +\ \frac{2}{6}\cdot0=0\]
\[G_3\ =\ 0.92\ -\ 0\ =\ 0.92\]
Підсумуємо результати обчислень у таблиці 1.
| Розбиття № | Початкова ентропія | Зважена ентропія | Інформаційний приріст |
| 1 | 0.92 | 0.46 | 0.46 |
| 2 | 0.92 | 0.6 | 0.32 |
| 3 | 0.92 | 0 | 0.92 |
Третій варіант поділу даних є оптимальний, оскільки інформаційний приріст такого поділу – максимальний. Незважаючи на те, що, на перший погляд, перший та другий варіанти поділу виглядають схожими (лише по-одій кульці іншого кольору в групі), саме перший варіант усуває більше невизначеності із розподілу (0.46 проти 0.32). Таким чином, що більша величина інформаційного приросту то більше ентропії (невизначеності) було видалено під час поділу. Так, наприклад, ідеальний поділ матиме приріст інформації рівний 0 оскільки він призводить до найбільш однорідних підмножин даних після розділення. Іншими словами, добрий поділ – це такий поділ, який розбиває дані на групи, де екземпляри в кожній групі схожі за відношенням до залежної змінної (target variable) (у цьому випадку – кольору кульок).
Приріст інформації у Деревах Рішень.
При побудові Дерева Рішень (Decision Tree) метод визначення приросту інформації використовують для вибору оптимальної незалежної змінної (features, dependent variables) на кроці побудови дерева.
Нехай дано навчальний масив даних який складається із трьох незалежних категорійних змінних (X,Y,Z) та однієї залежної категорійної змінної з двома можливими значеннями (CLASSTYPE 1,2).
| X | Y | Z | CLASSTYPE |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 2 |
| 1 | 0 | 0 | 2 |
Обчислимо початкову (батьківську) ентропію масиву даних, а також ентропії розподілів для кожної незалежної змінної.
\[E_{parent\ }=-1\cdot\left(\frac{2}{4}\log_2\left(\frac{2}{4}\right)\ +\frac{2}{4}\log_2\left(\frac{2}{4}\right)\right)\ =-1\ \cdot\left(-0.5\ -0.5\right)\ =\ 1\ \]
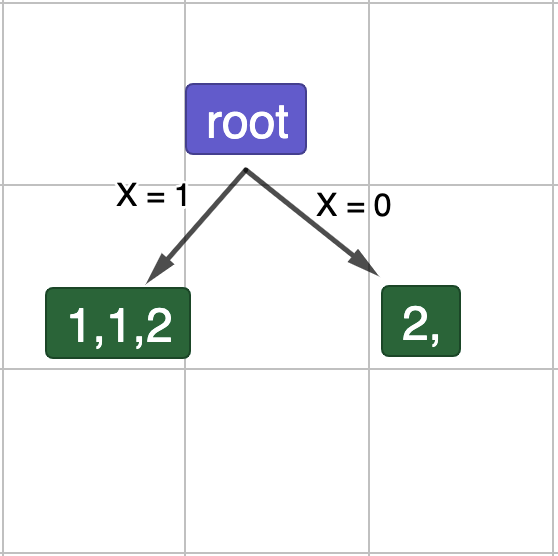
Рис.5. Поділ даних по X.
\[E_{child}\left(X=1\right)\ =-1\cdot\left(\frac{2}{3}\log_2\left(\frac{2}{3}\right)+\frac{1}{3}\log_2\left(\frac{1}{3}\right)\right)\ =\ 0.39\ +\ 0.53\ =\sim0.91\ \]
\[E_{child}\left(X=0\right)\ =\ -1\cdot\log_2\left(\frac{1}{1}\right)\ =\ -1\cdot0\ =\ 0\]
\[G\left(X\right)=1\ -\ E_{split}=1-\left(\left(\frac{3}{4}\cdot0.91\right)+\left(\frac{1}{4}\cdot0\right)\right)\ =\ \sim0.32\]
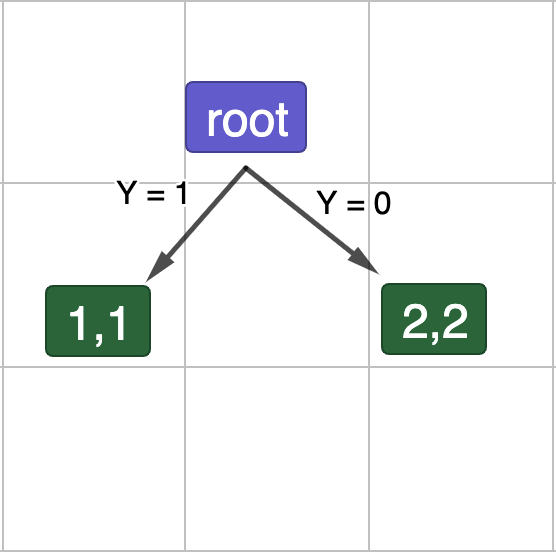
Рис.6. Поділ даних по Y.
\[E_{child}\left(Y=1\right)\ =-1\cdot\left(\frac{2}{2}\log_2\left(\frac{2}{2}\right)+\frac{2}{2}\log_2\left(\frac{2}{2}\right)\right)\ =\ -1\cdot\left(1\cdot0+1\cdot0\right)\ =\ 0\]
\[E_{child}\left(Y=0\right)\ =-1\cdot\left(\frac{2}{2}\log_2\left(\frac{2}{2}\right)+\frac{2}{2}\log_2\left(\frac{2}{2}\right)\right)\ =\ -1\cdot\left(1\cdot0+1\cdot0\right)\ =\ 0\]
\[G\left(Y\right)=1\ -\ E_{split}=1-\left(\left(\frac{2}{4}\cdot0\right)+\left(\frac{2}{4}\cdot0\right)\right)\ =\ 1\]
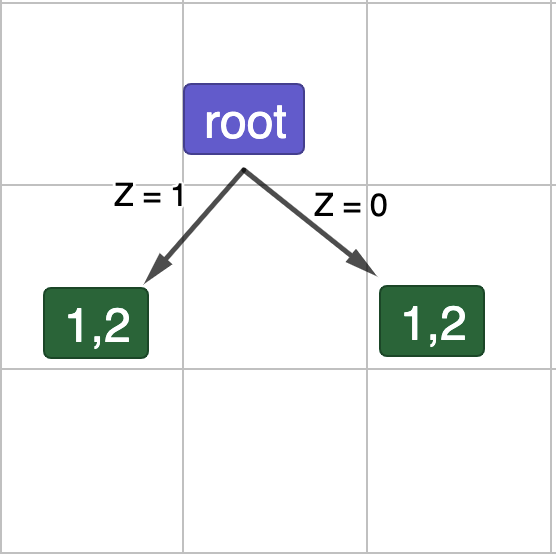
Рис.7. Поділ даних по Z.
\[E_{child}\left(Z=1\right)\ =-1\cdot\left(\frac{1}{2}\log_2\left(\frac{1}{2}\right)+\frac{1}{2}\log_2\left(\frac{1}{2}\right)\right)\ =\ 0.5\ +\ 0.5\ =1\]
\[E_{child}\left(Z=0\right)\ =-1\cdot\left(\frac{1}{2}\log_2\left(\frac{1}{2}\right)+\frac{1}{2}\log_2\left(\frac{1}{2}\right)\right)\ =\ 0.5\ +\ 0.5\ =1\]
\[G\left(Z\right)=1\ -\ E_{split}=1-\left(\left(\frac{2}{4}\cdot1\right)+\left(\frac{2}{4}\cdot1\right)\right)\ =\ 0\]
Як видно з розрахунків, найбільший приріст інформації досягається при поділі масиву даних за допомогою незалежнохї змінної Y із значенням 1. Тиким чином, перший лист в нашому дереві рішення після кореня буде Y = 1. Найменш ефективний поділ – за допомогою незалежнохї змінної Z. В цьому випадку приріст інфомації рівний 0.